コラム

これから説明する数学の問題を通じて、丁寧に説明するという挑戦をしてみようと思います。また、多くの問題を解くことで、課題に対する最適解を高速で導き出す道筋を得られるということも説明したいと思っています。

 

個人的な話で恐縮ですが、私は社会人になってから数学への興味が湧き、中年になった今でも、オンラインや書籍で小学校の算数、中高の数学の問題や解説に触れては、飽きもせずビジネスの課題に置き換えることが出来ないか……そんなことばかり考えています。

 

私の数少ない趣味の一つです。

ただ、一言断っておくと、決して専門的に数学を学んだわけではありません。単に「好き」というだけのものです。

 

さて、私をよく知る友人から、とても興味深い問題を教えてもらいましたので、以下にご紹介します（思い返しながらですので、不足があることはご了承ください）。

 

 

まずは頭の中で考えていただき、その次に実際にペンを取って紙に書きながら解いてみてください。

 

—＜シンキング・タイム＞—

 

 

いかがでしょうか。すぐ答えは出たでしょうか？

 

私は、問題を解いた後 冷静によく考え直してみると、「これ、見直してみると とても簡単な問題だよな・・・」となりました。その落差がとても興味深かったのでシェアします。

 

私がこの問題を解いた手順を説明します。

 

まず、

グッピ－が何匹なのかを明確にしたいですよね。

 

全体200匹のうちの99％ですから、以下の式で表せます。

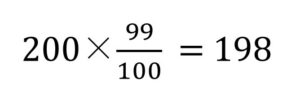
全体200匹のうち９９%を占めるグッピ－は１９８匹と判明しました。

 

ということは、残りの１%は別の魚２匹となります。

 

では、あらためて 問いについて考えてみます。

 

 

考え方の手順を考えて、式に表してみたいと思います。

 

グッピ－198匹からグッピ－x匹を取り除いた結果、全体に占めるグッピ－の割合が98％になればいいわけですよね。

 

【現状】

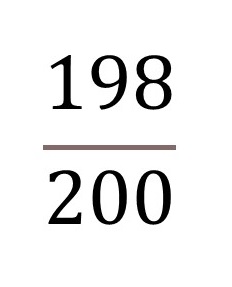
グッピ－を取り除く、ということは全体の数（分母）からもグッピ－の数（分子）からも取り除く必要がありますよね。

 

式で表すと、

 

【事後】

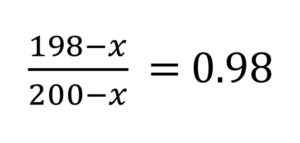
ということになります。

左辺の分母（200－x）を両辺に掛けて約分すると、

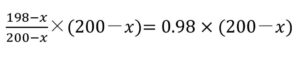
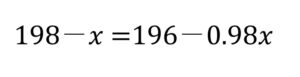
小数点がややこしいので、整数にするために両辺に100を掛けます。

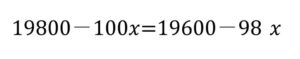
x の答えを導きます。

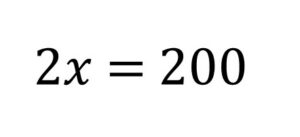
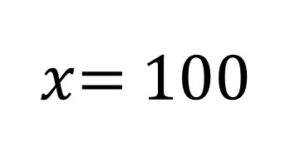
答えは、

200匹の魚がいる水槽からグッピ－を100匹取り除けば、グッピ－の占める割合は全体の98%になる、です。

 

どうでしょうか。

文章でわかりやすく解き方を説明できているでしょうか？

 

ビジネスの場面では、相手に対して正確に情報を伝え、更に自分の考え方を伝えるのはとても難しいです。

 

定性的な情報もうそうですが、定量的な情報処理に苦手意識を持っていればなおさら難しく感じるのではないでしょうか。

 

そしてどうでしょう、100匹という結果に、意外に思われた方も多いのではないでしょうか（違ったらスミマセン）。

 

私の周りの人たちに この質問をしたときも、2匹や4匹、という答えが返ってくることが多かったです。

 

計算力に優れた人ならば難なく解ける問題だと思います。しかし、私は はじめから順を追って計算式を考えないと解けませんでした。

 

この問題をあらためて振り返ると、取り除く数を2匹や4匹ぐらいかな？と考えた人は、グッピ－（分子）を取り除いたら同時に水槽の魚の数（分母）が減ることを見落としていませんでしたか？さらに、割合（％）と実数（匹）の数値を揃えればよかったことに気付きませんか？（以下で説明します）

 

この問題を一瞬で頭の中で解いた人は恐らく、

• グッピ－以外の魚の数は2匹のままである。
• グッピ－が98%になるということは、別の魚は2%である。
• 別の魚が2匹なら、グッピ－は98匹となる
• 198匹のグッピ－から98匹にするには、100匹を取り除けばいい

といったように、別の魚の数2匹と目指すパ－センテ－ジの2%の一致を活かして簡単に解きやすくしているのではと思います。

 

このような問題をササっと解ける人たちは、おそらくですが、過去に同じような問題に数多く触れ、かつ繰り返し接してきたことで 構造的な理解に加え、ショートカット的に解答パタ－ンを色々と知っているのだろうと思うのです。

 

ちなみにですが、私がこのグッピ－の問題を解き終わったあと友人いわく「Microsoft社の入社試験問題らしいよ」とのことでした（真偽は確かめていません）。

 

思考力が試されることは当然のことですが、説明力を鍛えるためのトレ－ニングにも最適な問題ではないでしょうか。

 

▼

他に、以下のような問題があることもご紹介しておきます。

 

 

直感的に、数キロは必要だろう…と思った方も多いのではないでしょうか。

 

今回ご紹介した問題を通じて私がお伝えしたいことは、説明力の大切さとあわせて、自分の直感が通じる世界なんてものは 所詮は自分が対応可能なスケールの範囲内だけであり、それを超える直感はデタラメになりかねないことを理解しておくことが賢明だということです。

 

『直感的直感』と『論理的直感』の違い、そんな言葉に集約されるかもしれません（しらんけど…（笑））。

 

経営者の経験と勘と度胸、いわゆるKKDがこれからの未来に果たしてどれほど通じるのだろうか……など思いを巡らせると話は尽きません。

 

まだ他にも興味深い数学の問題がありますが、今回はひとまずこれぐらいで終わります。

 

参謀学Lab.研究員 青木 永一

 

（ 答：約6.28m ）